Limitaciones

El Método de Diseño Directo sólo es aplicable cuando se satisfacen las limitaciones ilustradas en la Figura 19-2:

1. En cada dirección debe haber tres o más tramos continuos;

2. Los paneles de losa deben ser rectangulares, con una relación entre la luz mayor y la luz menor (medidas entre los centros de
los apoyos) no mayor que 2;

3. Las longitudes de las luces sucesivas en cada dirección (medidas entre los centros de los apoyos) no deben diferir en más de
1/3 de la luz mayor;

4. Las columnas no deben estar desalineadas respecto de cualquier eje que une centros de columnas sucesivas más de 10% de la luz (en la dirección del desalineamiento);

5. Las cargas deben ser uniformemente distribuidas, y la sobrecarga no mayorada o de servicio no debe ser mayor que dos veces
la carga permanente no mayorada o de servicio (L/D ≤ 2);

6. Para las losas en dos direcciones con todos sus lados apoyados en vigas, la rigidez relativa de las vigas en dos direcciones perpendiculares debe satisfacer los requisitos mínimos y máximos especificados en el artículo 13.6.1.6; y

7. No está permitida la redistribución de momentos negativos de acuerdo con el artículo 8.4.

DISEÑO PRELIMINAR

Antes de proceder con el Método de Diseño Directo es necesario determinar una altura de losa preliminar h para controlar las flechas, de acuerdo con los requisitos de altura mínima dados en el artículo 9.5.3. Tanto la Tabla 18-1 como la Figura 18-3 se pueden utilizar para simplificar el cálculo de la altura mínima.


Para los sistemas de losas sin vigas, en esta etapa del proceso de diseño es aconsejable verificar la resistencia al corte de la losa en la proximidad de las columnas u otros apoyos de acuerdo con el requisito especial para el corte en losas (11.12). Ver la discusión sobre el artículo 13.5.4 en la Parte 18.

Una vez que se ha seleccionado una altura de losa, el Método de Diseño Directo, el cual básicamente consiste en un procedimiento de análisis en tres pasos, implica: (1) determinar el momento estático mayorado total para cada tramo, (2) dividir el momento estático mayorado total en un momento positivo y otro momento negativo en cada tramo, y (3) distribuir los momentos positivos y negativos a las franjas de columna y las franjas intermedias en la dirección transversal.

Para efectuar el análisis el sistema de losas se divide en franjas de diseño compuestas por una franja de columna más dos medias franjas intermedias, según lo definido en los artículos 13.2.1 y 13.2.2 y como se ilustra en la Figura 19-1. En el caso de los sistemas de losas en los cuales las longitudes de tramo varían a lo largo de la franja de diseño, el diseñador deberá aplicar su criterio profesional para aplicar las definiciones dadas en el artículo 13.2.1.

Losas en dos direcciones - Método de Diseño Directo

CONSIDERACIONES GENERALES

El Método de Diseño Directo es un procedimiento aproximado para analizar sistemas de losas en dos direcciones solicitados exclusivamente por cargas gravitatorias. Debido a que se trata de un procedimiento aproximado, la aplicación de este método se limita a los sistemas de losas que satisfacen las limitaciones especificadas en el artículo 13.6.1. Los sistemas de losas en dos direcciones que no satisfacen estas limitaciones se deben analizar mediante procedimientos más exactos tal como el Método del Pórtico Equivalente especificado en 13.7. En la Parte 20 presentamos una discusión del Método del Pórtico Equivalente, junto con ejemplos de diseño.

Con la publicación de ACI 318-83, el Método de Diseño Directo simplificó enormemente el análisis de los momentos de los sistemas de losas en dos direcciones, ya que se eliminaron todos los cálculos de las rigideces para determinar los momentos de diseño en un tramo extremo. Las expresiones para calcular la distribución en función de la relación de rigidez αec fueron reemplazadas por una tabla de coeficientes de momento para distribuir los momentos totales en los tramos finales (13.6.3.3). Otro cambio introducido fue que la anterior ecuación aproximada (13-4) para transferencia de momento no balanceado entre la losa y
una columna interior también se simplificó, eliminando el término de αec. A partir de estos cambios el Método de Diseño Directo se transformó en un procedimiento de diseño verdaderamente directo, uno que permite determinar todos los momentos de diseño mediante la aplicación de coeficientes de momento. Además, se incorporó un nuevo artículo 13.6.3.6, que contiene un requisito especial para el corte debido a la transferencia de momento entre una losa sin vigas y una columna de borde, y que se aplica cuando se utilizan los coeficientes de momento aproximados de 13.6.3.3. Ver la discusión del artículo 13.6.3.6 a continuación. Hasta la edición 1989 del Código (revisada en 1992), el artículo R13.6.3.3 incluía un "Método de Rigidez Modificado" que reflejaba la distribución original, y que permitía confirmar que las ayudas para el diseño y el software basados en la distribución original en función de la relación de rigidez αec aún eran aplicables. El "Método de Rigidez Modificado" se eliminó del artículo R13.6.3.3 en la edición 1995 del Código y el comentario.

A.1 DEFINICIONES (I)

El procedimiento de diseño por bielas y tirantes exige diferenciar en los elementos de hormigón dos tipos de zonas, dependiendo de las características de los campos de tensiones en cada ubicación. En consecuencia, los elementos estructurales se dividen en regiones B y regiones D.

Regiones B - Las regiones B representan las partes de un elemento en las cuales se puede aplicar la hipótesis de "secciones planas" de la teoría clásica de flexión.
Regiones D - Las regiones D son las partes de un elemento que están ubicadas fuera de las regiones B; en las regiones D se anticipa que luego de aplicar las cargas las secciones planas no permanecerán planas. Típicamente se asume que hay regiones D en las partes de un elemento donde hay discontinuidades (o perturbaciones) de la distribución de tensiones provocadas por la presencia de fuerzas concentradas (cargas o reacciones) o cambios bruscos de la geometría. En base al principio de St. Venant, las tensiones normales (debidas a carga axial y flexión) se aproximan a una distribución prácticamente lineal a una distancia aproximadamente igual al mayor valor entre la altura total (h) y el ancho del elemento, a partir de la ubicación de la fuerza concentrada o la irregularidad geométrica. La Figura 17-1 ilustra ejemplos típicos de discontinuidades, Regiones D (áreas sombreadas) y Regiones B.

REQUISITOS GENERALES

El modelo de bielas y tirantes constituye un enfoque de diseño nuevo, aplicable a toda una gama de problemas de diseño para los cuales el cuerpo principal del código no contiene una solución de diseño explícita. Este método exige que el diseñador seleccione cuidadosamente un recorrido realista de las cargas dentro del elemento estructural, formando un reticulado idealizado. Detallando los elementos del reticulado de forma racional y satisfaciendo las condiciones de equilibrio se asegura la transferencia de las cargas a los apoyos o a otras regiones diseñadas mediante métodos convencionales. Aunque las soluciones que se obtienen aplicando esta poderosa herramienta de análisis no son únicas, representan un enfoque conservador de límite inferior. A diferencia de algunas de las formulaciones contenidas en el cuerpo principal del Código, el modelo racional y fácil de visualizar indicado en el Apéndice A permite comprender las necesidades de diseño de las regiones irregulares de las estructuras de hormigón, a la vez que promueve la ductilidad.

La metodología de diseño presentada en el Apéndice A se basa en gran medida en los artículos preparados sobre este tema por Schlaich et al.17.1 y Marti17.2. A partir de la publicación de estos trabajos, el método de bielas y tirantes ha recibido cada vez mayor atención por parte de otros investigadores y autores (Collins y Mitchell17.3, MacGregor17.4). La forma actual del Apéndice A no incluye requisitos explícitos sobre comportamiento en servicio (tal como control de las flechas o fisuración).

Modelos de Bielas y Tirantes

ACTUALIZACIÓN PARA EL CÓDIGO 2002

La edición 2002 del Apéndice A de ACI 318 introduce la forma codificada del método de bielas y tirantes. Aunque las analogías del reticulado estaban implícitas en los requisitos de diseño para corte y torsión de las ediciones anteriores del Código, y se permitía utilizar "métodos que satisfacen los requisitos de equilibrio y resistencia," esta es la primera vez que el tema es tratado de manera consistente.

ENTALLADURAS HORIZONTALES EN VIGAS (I)

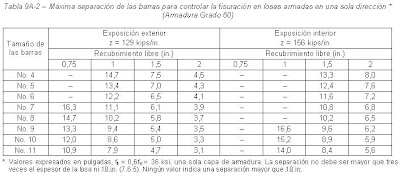
Las vigas que tienen entalladuras horizontales se deben diseñar para los efectos globales de flexión, corte, esfuerzos axiales y torsión que actúan en el elemento, como así también para los efectos locales en la proximidad de la entalladura (Referencias 15.2 y 15.6). El Código no trata específicamente el diseño de las entalladuras horizontales en vigas. Esta sección sólo abarca los modos de falla localizados y los requisitos de armadura para impedir estas fallas.

El diseño de las entalladuras de las vigas es similar al de las ménsulas en cuanto a las condiciones de carga, pero en las entalladuras de vigas se deben considerar requisitos de diseño y detalles de armado adicionales. En consecuencia, aún cuando el Código no lo trata específicamente, este capítulo presenta el diseño de las entalladuras horizontales en vigas. En la Figura 15-3 se ilustran
algunos de los modos de falla ya descritos al hablar de las ménsulas. Sin embargo, en el caso de las entalladuras se deberán
considerar dos modos de falla adicionales (ver Figura 15-3): (5) separación entre la entalladura y el alma de la viga cerca de la parte superior de la entalladura en la proximidad de la carga de la entalladura, y (6) punzonado. La carga vertical aplicada a la entalladura es resistida por una biela comprimida. A su vez, la componente vertical de la biela comprimida inclinada debe ser tomada por los estribos del alma (ramas de los estribos Av adyacentes a la cara lateral del alma) que actúan como armadura "de suspensión" para llevar la carga de la entalladura a la parte superior de la viga. En la esquina formada por la intersección de la entalladura y el alma aparecerá una fisura diagonal que se extenderá hasta el estribo y continuará adyacente al mismo. Por este motivo, para calcular el momento debido a Vu se utiliza una luz de corte, af, ligeramente mayor. Ahora bien, la sección crítica para el momento se toma en el centro de los estribos de la viga, y no en la cara de la viga. Además, para las entalladuras horizontales en
las vigas, para la resistencia a la flexión el brazo de momento interno no se debe tomar mayor que 0,8h.

Requisitos de diseño (II)

De acuerdo con el artículo 11.9.4, tanto en el caso (a) como en el caso (b), Ah 0, 5As An determina la cantidad de armadura de corte que se debe proveer en forma de estribos cerrados paralelos a As distribuidos en forma uniforme dentro de una distancia igual a (2/3 d) adyacente a As.

Se requiere una cuantía mínima de armadura principal de tracción ρmin = 0,04f´c/fy para asegurar un comportamiento dúctil una vez que se produce fisuración bajo la acción del momento y la fuerza de tracción directa (11.9.5).

Requisitos de diseño (I)

La sección crítica para el diseño de las ménsulas se toma en la cara del apoyo. Esta sección se debe diseñar para que resista simultáneamente un esfuerzo de corte Vu, un momento Mu = Vua + Nuc (h – d), y una fuerza de tracción horizontal Nuc (11.9.3). El valor de Nuc no debe ser menor que 0,2Vu, a menos que se adopten disposiciones especiales para evitar las fuerzas de tracción
(11.9.3.4). Este valor mínimo de Nuc se ha establecido para tomar en cuenta el comportamiento incierto de las uniones deslizantes y/o los apoyos flexibles. Además, típicamente la fuerza de tracción Nuc se debe a causas indeterminadas tales como la contracción restringida o las tensiones de origen térmico. En cualquier caso, esta fuerza se debe considerar siempre como una sobrecarga a la cual se aplicará un factor de carga igual a 1,6 (11.9.3.4). Debido a que el diseño de las ménsulas es controlado fundamentalmente por corte, el artículo 11.9.3.1 especifica que el factor de reducción de la resistencia, , se debe tomar igual a 0,75 para todas las condiciones de diseño.

Para el hormigón de peso normal, la resistencia al corte Vn se limita al menor valor entre 0,2f'cbwd y 800bwd (11.9.3.2). Para el hormigón liviano, Vn está limitada por los requisitos del artículo 11.9.3.2.2, los cuales son más restrictivos que los correspondientes a hormigón de peso normal. Ensayos realizados han demostrado que en el caso del hormigón liviano Vn depende
de f'c y de a/d.

Para las ménsulas la armadura requerida es:

Avf = área de armadura de corte por fricción para resistir el corte directo Vu, calculada de acuerdo con el artículo
11.7 (11.9.3.2).

Af = área de armadura de flexión para resistir el momento Mu = Vua + Nuc (h – d), calculada de acuerdo con los artículos 10.2 y 10.3 (11.9.3.3).

An = área de armadura para resistir la fuerza de tracción directa Nuc, calculada de acuerdo con el artículo 11.9.3.4.

En la Figura 15-2 se ilustra la armadura que se debe proveer, incluyendo:

As = armadura principal de tracción

Ah = armadura de corte (estribos cerrados)

Esta armadura se provee de manera tal que la armadura total As + Ah que atraviesa la cara del apoyo sea el valor mayor entre (a)
Avf + An, y (b) 3Af /2 + An para satisfacer criterios basados en resultados de ensayos.15.1

Torsión crítica (III)

Es importante observar que si se trata de secciones huecas en las Ecuaciones (12) a (14) se debe utilizar Ag en lugar de Acp.
Para el análisis de la torsión, una sección hueca se define como aquella que posee uno o más vacíos longitudinales de manera
que se verifique Ag/Acp < 0,95 (ver R11.6.1). En este caso el término Ag es el área de hormigón solamente (es decir, no incluye
el área de los vacíos), en base a la sección establecida en el artículo 13.2.4. En el Código 2002 se modificaron los requisitos del
artículo 11.6.1 de manera que se puedan aplicar a secciones huecas, ya que los ensayos informados en la Referencia 11.29 indican que el momento torsor de fisuración de una sección hueca es aproximadamente (Ag/Acp) por el momento torsor de fisuración de una sección maciza que tiene las mismas dimensiones exteriores.

Torsión crítica (II)

Torsión crítica (I)

La torsión se puede despreciar si el momento torsor mayorado Tu es menor que Tcr/4, siendo Tcr el momento torsor de fisuración (o momento torsor crítico). El momento torsor de fisuración corresponde a una tensión de tracción principal de
4 f 'c . Antes de la fisuración, el espesor de la pared del tubo "t" y el área encerrada por la trayectoria del flujo de corte "Ao" se relacionan con la geometría de la sección no fisurada en base a las siguientes hipótesis:


Las Ecuaciones (7) y (8) se aplican a secciones no fisuradas. Para las vigas de borde y otros elementos hormigonados de forma monolítica con una losa, el ancho de ala en voladizo de la losa contribuyen a la resistencia a la torsión. En la Figura R13.2.4 se ilustra la sección efectiva de losa a considerar junto con la viga.



Reemplazando t de la Ecuación (7), Ao de la Ecuación (8) y tomando 4 f 'c
momento torsor de fisuración para los elementos no pretensados:

Longitud sin apoyo lateral y longitud efectiva de elementos comprimidos (III)

En las estructuras habituales de hormigón armado el diseñador rara vez se ocupa de elementos individuales, sino que analiza sistemas aporticados rígidos compuestos por conjuntos de viga-columna y losa-columna. El comportamiento de pandeo de un pórtico que no está arriostrado contra el desplazamiento lateral (desplazable) se puede ilustrar mediante el pórtico sencillo de la Figura 11-9. Como no tiene restricción lateral en el extremo superior, la totalidad del pórtico (no arriostrado) es libre de moverse lateralmente. El extremo inferior puede ser articulado o estar parcialmente restringido contra la rotación. En general, la longitud efectiva ℓe depende del grado de restricción contra la rotación de los extremos de la columna y ℓu < ℓe < ∞.

Longitud sin apoyo lateral y longitud efectiva de elementos comprimidos (II)

Una columna que está empotrada en un extremo y totalmente libre en el otro (en voladizo) pandeará como se ilustra en la Figura 11-8(a). El extremo superior tendrá un desplazamiento lateral relativo con respecto al extremo inferior. La geometría deformada de estos elementos es similar a la mitad de la deformada sinusoidal del elemento articulado en ambos extremos ilustrado en la Figura 11-7(a). En consecuencia, la longitud efectiva es igual a dos veces la longitud real. Si la columna está impedida contra la rotación en ambos extremos pero uno de los extremos se puede desplazar lateralmente respecto del otro, la columna pandeará como
se ilustra en la Figura 11-8(b). La longitud efectiva ℓe será igual a la longitud real ℓu, con un punto de inflexión (pi) ubicado como se indica. La carga de pandeo de la columna de la Figura 11-8(b), en la cual el desplazamiento lateral no está impedido, es un cuarto de la de la columna de la Figura 11-7(b), en la cual el desplazamiento lateral sí está impedido. Como se indicó anteriormente, los extremos de las columnas rara vez son totalmente articulados o totalmente empotrados, sino que están parcialmente restringidos contra la rotación por los elementos solidarios a la columna. Por lo tanto, la longitud efectiva variará entre ℓu e infinito, como se indica en la Figura 11-8(c). Si los elementos que restringen el movimiento (vigas o losas) son muy rígidos en relación con la columna, el pandeo se aproximará al esquema ilustrado en la Figura 11-8(b). En cambio, si los elementos que restringen el movimiento son bastante flexibles, la columna se aproximará a una condición articulada en ambos extremos y la columna (o las columnas), y posiblemente la estructura, se aproximarán a la instabilidad.

Longitud sin apoyo lateral y longitud efectiva de elementos comprimidos (I)

La longitud sin apoyo lateral (o longitud no soportada) ℓu de una columna, definida en 10.11.3, es la distancia libre entre apoyos laterales, como se ilustra en la Figura 11-6. Observar que la longitud ℓu puede ser diferente para el pandeo respecto de cada uno de los ejes principales de la sección transversal de la columna. La ecuación básica de Euler para la carga crítica de pandeo se puede expresar como Pc = π2EI/(ℓe)2, siendo ℓe la longitud efectiva kℓu. Las ecuaciones básicas para el diseño de columnas esbeltas fueron desarrolladas para extremos articulados y, por lo tanto, se las debe modificar para considerar los efectos de las condiciones de vínculo. La longitud efectiva de la columna, kℓu, y no la longitud real sin apoyo lateral ℓu, es la que se utiliza para estimar las resistencias de las columnas esbeltas. Esta longitud efectiva considera tanto las condiciones de vínculo como la condición de sistema indesplazable o desplazable.


Cuando se produce la carga crítica definida por la ecuación de Euler, un elemento originalmente recto pandea con una forma de semionda sinusoidal, como se ilustra en la Figura 11-7(a). Con esta configuración, en cada sección actúa un momento adicional P- ∆, siendo ∆ el desplazamiento lateral en el punto específico considerado a lo largo de la columna. Este desplazamiento lateral continúa aumentando hasta que la tensión por flexión provocada por el momento (P-∆), más la tensión de compresión original provocada por las cargas aplicadas, excede la resistencia a la compresión del hormigón y la columna falla. La longitud efectiva ℓe (= kℓu) es la longitud entre los apoyos articulados, entre puntos de momento nulo o entre puntos de inflexión. Para la condición de ambos extremos articulados ilustrada en la Figura 11-7(a), la longitud efectiva es igual a la longitud sin apoyo lateral o no soportada, ℓu. Si el elemento está empotrado en ambos extremos (restringido contra la rotación), el pandeo se producirá en la forma ilustrada en la Figura 11-7(b); habrá puntos de inflexión en los puntos indicados, y la longitud efectiva ℓe será igual a la mitad de la longitud sin apoyo lateral, ℓu. La carga crítica de pandeo Pc para la condición de extremos empotrados es cuatro veces mayor que para la condición de extremos articulados. En las estructuras reales rara vez las columnas son perfectamente articuladas o empotradas, sino que sus extremos están parcialmente restringidos contra la rotación por los elementos solidarios a la columna. En consecuencia, la longitud efectiva está comprendida entre ℓu/2 y ℓu, como se indica en la Figura 11-7(c), siempre que esté impedido el desplazamiento lateral de un extremo de la columna respecto del otro. El valor real de la longitud efectiva depende de la rigidez de los elementos solidarios a los extremos superior e inferior de la columna.

Apéndice 9A: Distribución de la armadura de tracción de acuerdo con el Código 1995 (IV) - REFERENCIA

REFERENCIA

9A.1 Lutz, L. A., "Crack Control Factor for Bundled Bars and for Bars of Different Sizes," ACI Journal, Proceedings Vol. 71, Enero 1974, pp. 9-10.

Final Distribución de la armadura de flexión

Apéndice 9A: Distribución de la armadura de tracción de acuerdo con el Código 1995 (III)

Para una sola capa de armadura, la separación máxima requerida para controlar la fisuración se determina de la siguiente manera (ver Figura 9A-3):



donde dc = recubrimiento libre + 1/2 (diámetro de barra). La ecuación anterior se utilizó para generar los valores para la máxima
separación de las barras indicados en las Tablas 9A-1 y 9A-2 para armadura Grado 60. Las tablas se basan en una tensión bajo
cargas de servicio fs = 0,6fy, según lo permitido por 10.6.4. Los cálculos para fs darían por resultado alrededor de 0,56fy para una relación entre sobrecarga y carga permanente igual a 0,5, y 0,60fy para una relación entre sobrecarga y carga permanente igual a 2.

SUPERFICIES DE FALLA

La resistencia nominal de una sección solicitada a flexión biaxial y compresión es una función de tres variables, Pn, Mnx y Mny, las cuales se pueden expresar en términos de una carga axial actuando con excentricidades ex = Mny/Pn y ey = Mnx/Pn, como se ilustra en la Figura 7-8. Una superficie de falla se puede describir como una superficie generada graficando la carga de falla Pn en función de sus excentricidades ex y ey, o de sus momentos flectores asociados Mny y Mnx. Se han definido tres tipos de superficies de falla.7.4, 7.5, 7.6 La superficie básica S1 se define mediante una función que depende de las variables Pn, ex y ey; esta superficie se ilustra en la Figura 7-9(a). A partir de S1 se puede derivar una superficie recíproca; para generar la superficie S2 (1/Pn, ex, ey) se utiliza la recíproca o inversa de la carga axial nominal Pn como se ilustra en la Figura 7-9(b). El tercer tipo de superficie de falla, ilustrado en la Figura 7-9(c), se obtiene relacionando la carga axial nominal Pn con los momentos Mnx y Mny para producir la superficie S3 (Pn, Mnx, Mny). La superficie de falla S3 es la extensión tridimensional del diagrama de interacción uniaxial que mencionamos anteriormente.

Varios investigadores han desarrollado aproximaciones tanto para la superficie de falla S2 como para la S3 que se pueden usar para el diseño y el análisis.7.6 - 7.10 A continuación presentamos una explicación de estos métodos utilizados en la práctica actual, junto

RESISTENCIA CON INTERACCIÓN BIAXIAL

Un diagrama de interacción uniaxial define la resistencia a la combinación de carga y momento en un único plano de una sección solicitada por una carga axial P y un momento uniaxial M. La resistencia a la flexión biaxial de una columna cargada axialmente se puede representar esquemáticamente como una superficie formada por una serie de curvas de interacción uniaxial trazadas en forma radial a partir del eje P (ver Figura 7-6). Los datos para estas curvas intermedias se obtienen variando el ángulo del eje neutro (para configuraciones de deformación específica supuestas) con respecto a los ejes principales (ver Figura 7-7).

La dificultad asociada con la determinación de la resistencia de las columnas armadas solicitadas a combinaciones de carga axial y flexión biaxial es fundamentalmente de naturaleza aritmética. La resistencia a la flexión de una columna cargada axialmente respecto de un eje oblicuo particular se determina mediante iteraciones que involucran cálculos sencillos pero laboriosos. Estos cálculos se vuelven aún más laboriosos si se desea optimizar la armadura o la sección transversal.

Para la flexión uniaxial es habitual utilizar ayudas de diseño en forma de curvas o tablas de interacción. Sin embargo, debido a la naturaleza voluminosa de los datos y a lo difícil que resulta realizar múltiples interpolaciones, no resulta práctico desarrollar curvas
o tablas de interacción para diferentes relaciones entre los momentos flectores respecto de cada eje. Por este motivo se han desarrollado varios enfoques (todos ellos basados en aproximaciones aceptables) que relacionan la respuesta de una columna en flexión biaxial con su resistencia uniaxial respecto de cada uno de sus ejes principales.