Cálculos y discusión - III

d. Rigidez torsional mayorada, Kta, debido a las vigas paralelas: Para las columnas interiores:

donde Is momento de inercia de la sección de losa ilustrada en la Figura 20-19.

264 63 / 12 4752 in.4
Isb momento de inercia de la totalidad de la sección T ilustrada en la Figura 20-19 y calculado con
ayuda de la Figura 20-21.

2, 72 14 203 / 1225.387 in.4

Figura 20-19 – Viga placa en la dirección de análisis

e. Rigidez de la columna equivalente, Kec :

donde

K ta

corresponde a dos elementos torsionales, uno a cada lado de la columna, y

Kc

corresponde a las columnas superior e inferior en la unión de la viga placa en un piso intermedio.

Para las columnas interiores:

Cálculos y discusión - II

c. Rigidez torsional de los elementos torsionales, Kt:

Para las columnas interiores:

C se toma como el mayor de los valores calculados con ayuda de la Tabla 19-2 para el elemento torsional
ilustrado en la Figura 20-17.

Figura 20-17 – Unión de un elemento torsional en una columna interior

Para las columnas exteriores:

donde C se calcula como el mayor de los valores calculados con ayuda de la Tabla 19-2 para el elemento
torsional ilustrado en la Figura 20-18.

Figura 20-18 – Unión de un elemento torsional en una columna exterior

Cálculos y discusión - I

1. Diseño preliminar para determinar la altura de la losa, h:

Control de las flechas: 9.5.3.3

Del Ejemplo 19.2, las relaciones entre las rigideces flexionales de las vigas y las losas, α, son:

α = 13,30 (viga de borde NS)

= 16,45 (viga de borde EW)

= 3,16 (viga interior NS)

= 3,98 (viga interior EW)

Debido a que todos los valores de α > 2,0 (ver Figura 8-2), la Ecuación (9-3) será determinante. Por lo tanto,

2. Elementos del pórtico equivalente.

Determinar las constantes de distribución de momentos y los coeficientes para los momentos en los extremos empotrados para los elementos del pórtico equivalente. Para analizar el pórtico parcial bajo cargas verticales
se utilizará el procedimiento de distribución de momentos. Los factores de rigidez, k, los coeficientes de continuidad, CC, y los factores para momento en los extremos empotrados, FEM, para las vigas placas y las columnas se determinan usando las tablas del Apéndice 20-A. A continuación presentamos estos cálculos.

a. Vigas placas, rigidez flexional en ambos extremos Ksb:

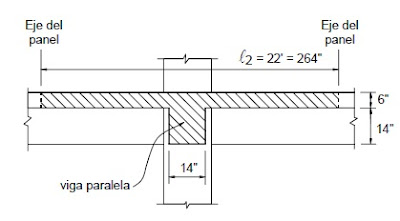
donde Isb es el momento de inercia de la sección de viga placa ilustrada en la Figura 20-16 y calculada con
ayuda de la Figura 20-21 incluida al final de este Ejemplo.

Figura 20-16 – Sección transversal de la viga placa

Aplicación del Método del Pórtico Equivalente a una losa en dos direcciones con vigas

Usando el método del Pórtico Equivalente, determinar los momento de diseño para el siguiente sistema de losa en la dirección
ilustrada, para un piso intermedio.

Altura de piso = 12 ft
Dimensiones de las vigas de borde = 14 × 27 in. Dimensiones de las vigas interiores = 14 × 20 in. Dimensiones de las columnas = 18 × 18 in. Sobrecarga de servicio = 100 lb/ft2

f'c = 4000 psi (para todos los elementos), hormigón de peso normal fy = 60.000 psi

Cálculos y discusión - X

A continuación se ilustran los detalles de armado correspondientes a una columna de borde.

iii. Determinar la armadura requerida para la franja intermedia. Proveer armadura mínima, ya que Mu = 0 (Ver Tabla 20-2)
Min. A 0, 0018 84 7 1, 06 in.2



Separación máxima smas 2h 14 in. 18 in.


En la franja intermedia colocar barras No. 4 con una separación de 14 in.

b. Verificar la tensión de corte combinada en la cara interna de la sección crítica de transferencia. 11.12.6.1

Las ecuaciones para la resistencia al corte se presentan en la el Capítulo 16 de este documento.

Del Ejemplo 19.1: Vu 25, 6 kips

Si los momentos mayorados se determinan mediante un método de análisis de pórtico exacto, tal como el
Método del Pórtico Equivalente, el momento no balanceado se toma directamente de los resultados del análisis de pórtico. Además, considerando la naturaleza aproximada del procedimiento de análisis de la transferencia de momentos, se asume que el momento no balanceado Mu actúa en el baricentro de la sección crítica de transferencia.

Por lo tanto, Mu 32, 3 ft-kips (Ver Tabla 20-2)

Cálculos y discusión - IX

ii. Verificar la armadura de la losa en la columna exterior para transferencia de momento entre la losa y la columna:

Porción del momento no balanceado transferido por flexión f Mu
De la Figura 16-13, Caso C:

Observar que se pueden utilizar los requisitos del artículo 13.5.3.3; sin embargo, en este ejemplo no los utilizamos.

Suponiendo que el comportamiento es controlado por la tracción, determinar el área de armadura requerida para f Mu 20,0 ft-kips

Ancho efectivo de la losa b c2 3h 16 3 7 37 in.

Por lo tanto, la sección es controlada por la tracción. 10.3.4

Proveer las 4 barras No. 4 requeridas concentrando 4 de las barras de la franja de columna (7 barras No. 4) en un ancho de losa de 37 in. sobre la columna. Por motivos de simetría agregar una barra No. 4 adicional fuera del ancho de 37 in.

Observar que la sección de la franja de columna continúa siendo controlada por la tracción, aún con la adición de una barra No. 4

Cálculos y discusión - VIII

Figura 20-15 – Momentos en las columnas (Momentos no balanceados de la viga placa)

8.   Verificar la resistencia a flexión de la losa y la resistencia al corte en una columna exterior

a.   Armadura total de flexión requerida para la franja de diseño:

i.    Determinar la armadura requerida para el momento de la franja de columna Mu  = 32,3 ft-kips

Suponer que se trata de una sección controlada por la tracción (f = 0,9)

Por lo tanto, la sección es controlada por tracción. 10.3.4

En la franja de columna usar 7 barras No. 4.

Cálculos y discusión - VII

7.   Momentos en las columnas:

El  momento  no  balanceado  de  las  vigas  placa  en  los  apoyos  del  pórtico  equivalente  se  distribuye  a  las columnas reales por encima y por debajo de la viga placa de forma proporcional a las rigideces relativas de las columnas. En base a la Figura 20-14, los momentos no balanceados en las uniones 1 y 2 son:

Unión 1 = + 46,5 ft-kips

Unión 2 = – 84,0 + 76,3 = – 7,7 ft-kips

En la Figura 20-15 se muestran las rigideces y los coeficientes de continuidad de las columnas reales, junto con la distribución de los momentos no balanceados a las columnas exteriores e interiores. Los momentos de diseño para las columnas se pueden tomar en la confluencia de la columna y la losa.

Resumiendo:

Momento de diseño en una columna exterior  = 22,08 ft-kips

Momento de diseño en una columna interior   = 3,66 ft-kips

Cálculos y discusión - VI

Momento total mayorado por tramo:


En los sistemas de losa comprendidos dentro de las limitaciones del artículo 13.6.1 los momentos resultantes
se pueden reducir en una proporción tal que no sea necesario que la sumatoria numérica de los momentos positivos y el promedio del momento negativo sea mayor que:

Se puede observar que con los momentos de diseño totales obtenidos aplicando el Método del Pórtico
Equivalente se obtiene un momento estático igual al dado por la expresión para momento estático usada con
el Método de Diseño Directo.

6. Distribución de los momentos de diseño en las franjas de la viga placa: 13.7.7.5

Los momentos mayorados negativos y positivos en las secciones críticas se pueden distribuir a la franja de columna y las dos semifranjas intermedias de la viga placa de acuerdo con las proporciones especificadas en
los artículos 13.6.4 y 13.6.6. El requisito del artículo 13.6.1.6 no se aplica en el caso de sistemas de losa sin vigas, α = 0. En la Tabla 20-2 se resume la distribución de los momentos mayorados en las secciones críticas.

* Para sistemas de losas sin vigas
** La porción del momento mayorado que no es resistido por la franja de columna se asigna a las dos semifranjas intermedias.

Cálculos y discusión - V

Distribución de momentos para el pórtico parcial

Notas:
* El momento de continuidad, MC, es el producto negativo entre el factor de distribución, el coeficiente de continuidad y el momento no balanceado de la unión que se transmite al extremo opuesto del tramo.
** El momento distribuido, MD, es el producto negativo entre el factor de distribución y el momento no balanceado de
la unión.
4. Momentos de diseño:


En la Figura 20-14 se grafican los momentos positivos y negativos mayorados para el sistema de losa en la
dirección de análisis. Los momentos de diseño negativos se toman en la cara de los apoyos rectilíneos pero a una distancia no mayor que 0,175ℓ1 a partir de los centros de los apoyos.

13.7.7.1



16 in.
 0, 67 ft 0,175 18 3, 2 ft
2

(Usar la ubicación de la cara del apoyo)

Figura 20-14 – Momentos de diseño positivos y negativos para la viga placa

(Todos los tramos cargados con la totalidad de la sobrecarga mayorada

Cálculos y discusión - IV

Rigidez de la columna equivalente, Kec.

donde

K t

corresponde a dos elementos torsionales, uno a cada lado de la columna, y

Kc

corresponde a las columnas superior e inferior en la unión de la viga placa en un piso intermedio.

e. Factores de distribución FD en la unión de la viga placa.

3. Análisis de pórtico parcial del pórtico equivalente:




Determinar los momentos negativos y positivos para las vigas placa usando el método de distribución de
momentos. Debido a que la sobrecarga de servicio no es mayor que tres cuartos de la carga permanente de servicio, se asume que los momentos de diseño ocurren en todas las secciones críticas considerando en todas
las luces la totalidad de la sobrecarga mayorada.

13.7.6.2

b. Distribución de momentos. La Tabla 20-1 muestra los cálculos. Los momentos antihorarios que actúan en los extremos del elemento se consideran positivos. Los momentos de tramo positivos se determinan a partir de la siguiente ecuación:

siendo Mo el momento a la mitad de la luz para una viga simple.

Si los momentos en los extremos no son iguales, el máximo momento del tramo no se produce en la mitad
de la luz, pero su valor es similar al correspondiente a la mitad de la luz. Momento positivo en el tramo 1-2:

Cálculos y discusión - III

b.   Rigidez flexional de las columnas en ambos extremos, Kc.

En base a la Tabla A7, Apéndice 20A,  t a  = 3,5 in., t b  = 3,5 in. ,

H = 9 ft = 108 in.; Hc  = 101 in.; ta  / t b  = 1; H / Hc  = 1, 07

Por lo tanto, por interpolación,  k AB  = k BA  = 4, 74

Rigidez torsional de los elementos torsionales, Kt.

Cálculos y discusión - II

Como no hay esfuerzos de corte en los ejes de los paneles adyacentes, la resistencia al corte en dos
direcciones a una distancia d/2 alrededor del apoyo se calcula de la siguiente manera:

Secciones críticas para el corte correspondientes al problema del Ejemplo

El diseño preliminar indica que una losa de 7 in. es adecuada para controlar las flechas y también para la resistencia al corte.

2. Elementos del pórtico equivalente:

Determinar los factores de distribución de momentos y los momentos en los extremos empotrados para los elementos del pórtico equivalente. Para analizar el pórtico parcial utilizaremos el procedimiento de distribución de momentos. Los factores de rigidez, los coeficientes de continuidad (CC) y los coeficientes para los momentos en los extremos empotrados (FEM) se determinan usando las tablas del Apéndice 20-A. A continuación ilustramos estos cálculos.

a. Rigidez flexional de las vigas placa en ambos extremos, Ksb.

El coeficiente de continuidad CC = 0,509 (por interpolación entre los valores de la Tabla A1).


El momento en el extremo empotrado FEM 0, 0843w

 2 , por interpolación en base a la Tabla A1

Cálculos y discusión - I

Diseño preliminar para determinar la altura de la losa, h:
a. Control de las flechas.
Para un sistema de placas planas, la mínima altura total, h, con armadura Grado 60 es 9.5.3.2
(ver Tabla 18-1):

pero no menor que 5 in.                                                                                                                                                           9.5.3.2(a)         

donde ℓn  = longitud de la luz libre en la dirección más larga = 216 – 16 = 200 in. Intentar con una losa de 7 in. para todos los paneles (peso = 87,5 lb/ft2)

b.   Resistencia al corte de la losa.

Usar una altura efectiva promedio, d = 5,75 in. ( recubrimiento de 3/4 in. y barras No. 4)

Para el corte en una dirección (comportamiento como viga ancha) considerar una franja de 12 in. de ancho
a una distancia d medida a partir de la cara del apoyo en la dirección más larga (ver Figura 20-13).

AYUDAS PARA DETERMINAR LAS CONSTANTES DE DISTRIBUCIÓN DE MOMENTOS - VI

Usar  el  Método  del  Pórtico  Equivalente  para  determinar  los  momentos  de  diseño  para  el  sistema  de  losa  en  la  dirección

ilustrada, para un piso intermedio.

Altura de piso = 9 ft

Dimensiones de las columnas = 16 × 16 in.

Las cargas laterales serán resistidas por muros de cortante

No hay vigas de borde

Peso de los tabiques no estructurales = 20 lb/ft2

Sobrecarga de servicio = 40 lb/ft2

f'c  = 4000 psi (losas), hormigón de peso normal

f'c  = 6000 psi (columnas), hormigón de peso normal fy = 60.000 psi